Coefficient de détermination
Le coefficient de détermination est une mesure utilisée dans l’analyse statistique pour évaluer dans quelle mesure un modèle explique et prédit les résultats futurs. Cela indique le niveau de variabilité expliquée dans l’ensemble de données. Le coefficient de détermination, également appelé « R au carré », sert de guide pour mesurer la précision du modèle.
Une façon d’interpréter cette figure est de dire que les variables incluses dans un modèle donné expliquent environ x% de la variation observée. Donc, si R2 = 0,50, environ la moitié de la variation observée peut être expliquée par le modèle.
Retenons
- Le coefficient de détermination est une idée complexe centrée sur l’analyse statistique d’un futur modèle de données.
- Le coefficient de détermination est utilisé pour expliquer combien la variabilité d’un facteur peut être causée par sa relation avec un autre facteur.
Comprendre le coefficient de détermination
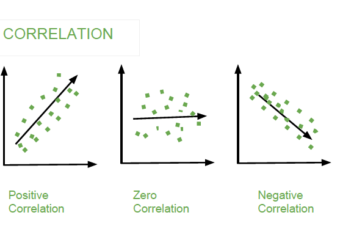
Le coefficient de détermination est utilisé pour expliquer combien la variabilité d’un facteur peut être causée par sa relation avec un autre facteur. Elle est largement utilisée dans l’analyse des tendances et est représentée par une valeur comprise entre 0 et 1.
Plus la valeur est proche de 1, meilleur est l’ajustement ou la relation entre les deux facteurs. Le coefficient de détermination est le carré du coefficient de corrélation, également appelé « R », ce qui lui permet d’afficher le degré de corrélation linéaire entre deux variables.
Cette corrélation est connue sous le nom de » qualité de l’ajustement « . Une valeur de 1,0 indique un ajustement parfait. Il s’agit donc d’un modèle très fiable pour les prévisions futures, indiquant que le modèle explique toutes les variations observées. Une valeur de 0, par contre, indiquerait que le modèle ne parvient pas à modéliser les données avec précision. Pour un modèle à plusieurs variables, par exemple un modèle de régression multiple, le R2 est un meilleur coefficient de détermination. En économie, une valeur de R2 supérieure à 0,60 est considérée comme intéressante.
Avantages de l’analyse du coefficient de détermination
Le coefficient de détermination est le carré de la corrélation entre les scores prévus dans un ensemble de données et l’ensemble réel des scores. Il peut également être exprimé comme le carré de la corrélation entre les scores X et Y, le X étant la variable indépendante et le Y étant la variable dépendante.
Indépendamment de la représentation, un R au carré égal à 0 signifie que la variable dépendante ne peut pas être prédite à l’aide de la variable indépendante. À l’inverse, s’il est égal à 1, cela signifie que la dépendance d’une variable est toujours prédite par la variable indépendante.
Un coefficient de détermination compris dans cette plage mesure la mesure dans laquelle la variable dépendante est prédite par la variable indépendante. Un R carré de 0,20, par exemple, signifie que 20% de la variable dépendante est prédite par la variable indépendante.
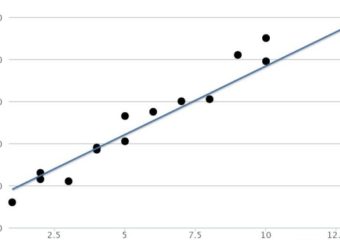
La qualité de l’ajustement, ou le degré de corrélation linéaire, mesure la distance entre une ligne ajustée sur un graphique et tous les points de données dispersés autour du graphique. Les données limitées auront une ligne de régression très proche des points et un niveau d’ajustement élevé, ce qui signifie que la distance entre la ligne et les données est très petite. Un bon ajustement a un R2 qui est proche de 1.
Cependant, R2 est incapable de déterminer si les points de données ou les prédictions sont biaisés. En outre, il n’indique pas à l’analyste ou à l’utilisateur si le coefficient de détermination est bon ou non. Un faible R2 n’est pas mauvais, par exemple, et il appartient à la personne de prendre une décision en fonction du nombre de R2.
Le coefficient de détermination ne doit pas être interprété naïvement. Par exemple, si le R au carré d’un modèle est signalé à 75%, la variance de ses erreurs est 75% inférieure à la variance de la variable dépendante et l’écart type de ses erreurs est 50% inférieur à l’écart type de la variable dépendante. L’écart-type des erreurs du modèle représente environ un tiers de la taille de l’écart-type des erreurs que vous obtiendriez avec un modèle à constante uniquement.
Enfin, même si une valeur de R au carré est grande, il peut ne pas y avoir de signification statistique des variables explicatives dans un modèle, ou la taille effective de ces variables peut être très petite dans la pratique.