L’hétéroscédasticité
Qu’est-ce que l’hétéroscédasticité?
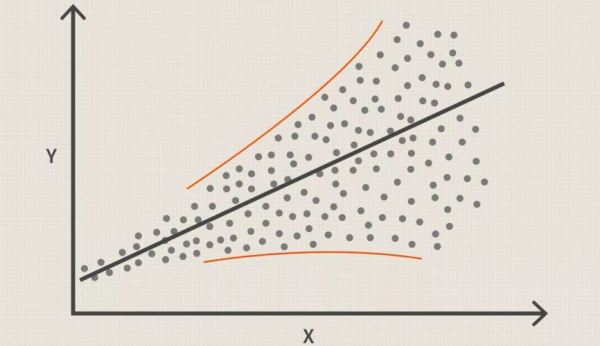
En statistique, l’hétéroscédasticité se produit lorsque les erreurs standard d’une variable, surveillées sur une durée déterminée, sont non constantes. Avec l’hétéroscédasticité, le signe révélateur de l’inspection visuelle des erreurs résiduelles est qu’elles tendent à se dissiper au fil du temps, comme illustré dans l’image ci-dessous.
L’hétéroscédasticité se présente souvent sous deux formes: conditionnelle et inconditionnelle. L’hétéroscédasticité conditionnelle identifie une volatilité non constante lorsque les périodes futures de forte et de faible volatilité ne peuvent pas être identifiées. L’hétéroscédasticité inconditionnelle est utilisée lorsqu’il est possible d’identifier des périodes à terme de forte et de faible volatilité.
Retenons
- En statistique, l’hétéroscédasticité (ou l’hétéroscédasticité) se produit lorsque les erreurs standard d’une variable, surveillées sur une durée déterminée, sont non constantes.
- Avec l’hétéroscédasticité, le signe révélateur de l’inspection visuelle des erreurs résiduelles est qu’elles tendent à se dissiper au fil du temps, comme illustré dans l’image ci-dessus.
- L’hétéroscédasticité est une violation des hypothèses retenues pour la modélisation par régression linéaire et peut donc avoir une incidence sur la validité de l’ analyse économétrique ou de modèles financiers tels que le MEDAF ( modèle d’évaluation des actifs financiers).
Bien que l’hétéroscédasticité ne cause pas de biais dans les estimations de coefficients, elle les rend moins précises; une précision inférieure augmente la probabilité que les estimations de coefficients soient plus éloignées de la valeur de population correcte.
Les bases de l’hétéroscédasticité
En finance, l’hétéroscédasticité conditionnelle est souvent constatée dans les prix des actions et des obligations. Le niveau de volatilité de ces actions ne peut être prédit sur aucune période. L’hétéroscédasticité inconditionnelle peut être utilisée lors de la discussion de variables présentant une variabilité saisonnière identifiable, telle que la consommation d’électricité.
En ce qui concerne les statistiques, l’hétéroscédasticité fait référence à la variance d’erreur, ou à la dépendance de la diffusion, dans au moins une variable indépendante d’un échantillon particulier. Ces variations peuvent être utilisées pour calculer la marge d’erreur entre des ensembles de données, tels que les résultats attendus et les résultats réels, car elles fournissent une mesure de l’écart des points de données par rapport à la valeur moyenne.
Pour qu’un ensemble de données soit considéré comme pertinent, la majorité des points de données doit se situer dans les limites d’un nombre particulier d’écarts-types par rapport à la moyenne, comme décrit par le théorème de Chebyshev, également connu sous le nom d’inégalité de Chebyshev. Ceci fournit des indications sur la probabilité d’une variable aléatoire différente de la moyenne.
En fonction du nombre d’écarts-types spécifiés, une variable aléatoire a une probabilité particulière d’exister à l’intérieur de ces points. Par exemple, il peut être nécessaire qu’une plage de deux écarts types contient au moins 75% des points de données pour être considérée comme valide. Une cause fréquente de variations en dehors des exigences minimales est souvent attribuée à des problèmes de qualité des données.
Le contraire de l’hétéroscédastique est l’homoscédastique. L’homoscédasticité fait référence à une condition dans laquelle la variance du terme résiduel est constante ou presque. L’homoscédasticité est une hypothèse de la modélisation par régression linéaire. L’homoscédasticité suggère que le modèle de régression peut être bien défini, ce qui signifie qu’il fournit une bonne explication de la performance de la variable dépendante.
Les types de l’hétéroscédasticité
Inconditionnel
L’hétéroscédasticité inconditionnelle est prévisible et concerne le plus souvent des variables cycliques par nature. Cela peut inclure des ventes au détail plus élevées pendant la période de magasinage des fêtes ou l’augmentation du nombre d’appels de réparation de climatiseurs pendant les mois les plus chauds.
Les changements dans la variance peuvent être directement liés à la survenue d’événements particuliers ou de marqueurs prédictifs si les changements ne sont pas traditionnellement saisonniers. Cela peut être lié à une augmentation des ventes de smartphones avec la sortie d’un nouveau modèle car l’activité est cyclique en fonction de l’événement mais pas nécessairement déterminée par la saison.
Conditionnel
L’hétéroscédasticité conditionnelle n’est pas prévisible par nature. Il n’existe aucun signe révélateur laissant croire aux analystes que les données deviendront plus ou moins dispersées à tout moment. Souvent, les produits financiers sont considérés comme soumis à l’hétéroscédasticité conditionnelle, car tous les changements ne peuvent pas être attribués à des événements spécifiques ou à des changements saisonniers.
Considérations particulières
Hétéroscédasticité et modélisation financière
L’hétéroscédasticité est un concept important dans la modélisation par régression et, dans le monde des investissements, des modèles de régression sont utilisés pour expliquer la performance des portefeuilles de titres et d’investissements. Le plus connu d’entre eux est le modèle d’évaluation des actifs financiers (MEDAF) qui explique la performance d’une action en termes de volatilité par rapport au marché dans son ensemble. Les extensions de ce modèle ont ajouté d’autres variables prédictives telles que la taille, le momentum, la qualité et le style (valeur par rapport à la croissance).
Ces variables explicatives ont été ajoutées car elles expliquent ou rendent compte de la variance de la variable dépendante. La performance du portefeuille est expliquée par le MEDAF. Par exemple, les concepteurs du modèle MEDAF savaient que leur modèle n’expliquait pas une anomalie intéressante: les actions de haute qualité, moins volatiles que les actions de faible qualité, avaient tendance à obtenir de meilleures performances que celles prédites par le modèle MEDAF. Selon le MEDAF, les actions à risque plus élevé devraient surperformer les actions à risque moins élevé. En d’autres termes, les actions à forte volatilité devraient battre les actions à plus faible volatilité. Cependant, les actions de haute qualité, moins volatiles, ont eu tendance à mieux performer que prévu par le MEDAF.
Plus tard, d’autres chercheurs ont étendu le modèle MEDAF (qui avait déjà été étendu pour inclure d’autres variables prédictives telles que la taille, le style et la quantité de mouvement) afin d’inclure la qualité en tant que variable prédictive supplémentaire, également appelée « facteur ». Avec ce facteur maintenant inclus dans le modèle, l’anomalie de performance des actions à faible volatilité a été prise en compte. Ces modèles, appelés modèles multi-facteurs , constituent la base de l’investissement factoriel et du bêta intelligent.