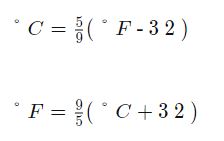Relation linéaire
Qu’est-ce qu’une relation linéaire?
Une relation linéaire (ou association linéaire) est un terme statistique utilisé pour décrire une relation linéaire entre une variable et une constante. Les relations linéaires peuvent être exprimées soit dans un format graphique où la variable et la constante sont connectées via une ligne droite, soit dans un format mathématique où la variable indépendante est multipliée par le coefficient de pente, ajouté par une constante, qui détermine la variable dépendante.
Une relation linéaire peut être contrastée avec une relation polynomiale ou non linéaire (courbe).
Retenons
- Une relation linéaire (ou association linéaire) est un terme statistique utilisé pour décrire une relation linéaire entre une variable et une constante.
- Les relations linéaires peuvent être exprimées sous forme graphique ou sous la forme d’une équation mathématique de la forme y = mx + b.
- Les relations linéaires sont assez courantes dans la vie quotidienne.
L’équation linéaire
Mathématiquement, une relation linéaire est celle qui satisfait l’équation: y = mx + b.
Où m est la pente et b l’ordonnée à l’origine.
Dans cette équation, «x» et «y» sont deux variables qui sont liées par les paramètres «m» et «b». Graphiquement, y = mx + b trace dans le plan xy comme une ligne avec la pente «m» et l’ordonnée à l’origine «b». L’ordonnée à l’origine «b» est simplement la valeur de «y» lorsque x = 0. La pente «m» est calculée à partir de deux points individuels (x 1 , y1 ) et (x2 , y2 ) comme:
m = ( y2 – y1) / ( x2 – x1)
Que vous dit une relation linéaire?
Une équation doit respecter trois ensembles de critères nécessaires pour être considérée comme linéaire: une équation exprimant une relation linéaire ne peut pas comprendre plus de deux variables, toutes les variables d’une équation doivent être à la première puissance et l’équation doit représenter graphiquement une ligne droite.
Une fonction linéaire en mathématiques est une fonction qui satisfait aux propriétés d’additivité et d’homogénéité. Les fonctions linéaires observent également le principe de superposition, qui stipule que la sortie nette de deux ou plusieurs entrées est égale à la somme des sorties des entrées individuelles. Une relation linéaire couramment utilisée est une corrélation, qui décrit comment une variable change de manière linéaire en changements dans une autre variable.
En économétrie, la régression linéaire est une méthode souvent utilisée pour générer des relations linéaires pour expliquer divers phénomènes. Cependant, toutes les relations ne sont pas linéaires. Certaines données décrivent des relations courbes (telles que les relations polynomiales) tandis que d’autres données ne peuvent pas être paramétrées.
Fonctions linéaires
Mathématiquement similaire à une relation linéaire est le concept d’une fonction linéaire. Dans une variable, une fonction linéaire peut s’écrire comme suit: f(x) = mx + b.
Où m est la pente et b l’ordonnée à l’origine.
Ceci est identique à la formule donnée pour une relation linéaire, sauf que le symbole f(x) est utilisé à la place de y. Cette substitution est faite pour mettre en évidence le sens que x est mappé sur f(x), alors que l’utilisation de y indique simplement que x et y sont deux quantités, liées par m et b.
Dans l’étude de l’algèbre linéaire, les propriétés des fonctions linéaires sont largement étudiées et rendues rigoureuses. Étant donné un scalaire C et deux vecteurs A et B de RN , la définition la plus générale d’une fonction linéaire indique que:
c×f(A+B)=c×f(A)+c×f(B)
Exemples de relations linéaires
Il existe aujourd’hui des équations utilisées dans le monde réel qui répondent à tous les critères discutés ci-dessus. Les relations linéaires sont très courantes dans notre vie quotidienne, même si nous n’en sommes pas conscients. Prenons, par exemple, la vitesse à laquelle les choses comme les voitures et les trains peuvent aller. Avez-vous déjà pensé à la façon dont leurs vitesses sont calculées? Lorsqu’un agent de police remet à quelqu’un une contravention pour excès de vitesse, comment sait-il avec certitude si la personne a accéléré? Eh bien, ils utilisent une relation linéaire simple appelée formule de taux .
Cette formule nous dit que la vitesse d’un certain objet est calculée en divisant la distance parcourue par le temps qu’il a fallu pour parcourir cette distance. Donc, si quelqu’un a passé 1 heure à parcourir une distance de 80 miles sur une route de 55 mph, alors vous pouvez être sûr qu’il accélérait car 80 miles divisés par 1 heure vous donne 80 mph. À première vue, cette formule semble ne pas correspondre aux critères car elle semble avoir trois variables. Mais, c’est vraiment une relation linéaire car au moins une de vos variables sera toujours une constante en fonction de votre problème. Vous pouvez avoir un taux constant pour lequel vous devez résoudre la distance ou le temps. La relation serait de 35 = d / t ou quel que soit le taux donné. C’est la même chose si la distance est donnée comme constante, r= 100 / t .
Un autre exemple est celui de la conversion de la température de Fahrenheit en Celsius. Afin de convertir Celsius en Fahrenheit, ou Fahrenheit en Celsius, vous utiliseriez les équations ci-dessous. Ces équations expriment une relation linéaire sur un graphique: