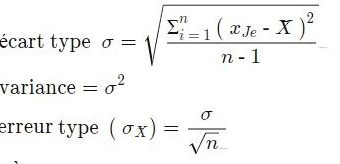Coefficient de variation (CV)
Le coefficient de variation (CV) est une mesure statistique de la dispersion des points de données dans une série de données autour de la moyenne. Le coefficient de variation représente le rapport entre l’écart type et la moyenne. Il s’agit d’une statistique utile pour comparer le degré de variation d’une série de données à une autre, même si les moyennes diffèrent radicalement les unes des autres.
Comprendre le coefficient de variation
Le coefficient de variation montre l’étendue de la variabilité des données d’un échantillon par rapport à la moyenne de la population. En finance, le coefficient de variation permet aux investisseurs de déterminer le degré de volatilité, ou de risque, pris en charge par rapport au montant de rendement attendu des investissements. Idéalement, la formule du coefficient de variation devrait aboutir à un ratio plus faible de l’ écart type sur le rendement moyen, ce qui signifie un meilleur compromis risque-rendement. Notez que si le rendement attendu du dénominateur est négatif ou égal à zéro, le coefficient de variation pourrait être trompeur.
Le coefficient de variation est utile lorsque vous utilisez le rapport risque / rendement pour sélectionner des investissements. Par exemple, un investisseur qui craint le risque peut vouloir prendre en compte des actifs présentant un degré de volatilité historiquement faible et un degré de rendement élevé, par rapport au marché ou à son secteur d’activité. Inversement, les investisseurs à la recherche de risques peuvent envisager d’investir dans des actifs présentant un degré de volatilité historiquement élevé.
Bien qu’ils soient le plus souvent utilisés pour analyser la dispersion autour de la moyenne, les CV par quartile, par quintile ou par décile peuvent également être utilisés pour comprendre la variation autour de la médiane ou du 10e centile, par exemple.
La formule ou le calcul du coefficient de variation peut être utilisé pour déterminer la variance entre le prix moyen historique et l’évolution du prix actuel d’une action, d’une marchandise ou d’une obligation.
Retenons
- Le coefficient de variation (CV) est une mesure statistique de la dispersion des points de données dans une série de données autour de la moyenne.
- En finance, le coefficient de variation permet aux investisseurs de déterminer le degré de volatilité ou de risque pris en compte par rapport au montant de rendement attendu des investissements.
- Plus le rapport entre l’écart type et le rendement moyen est faible, meilleur sera le compromis risque-rendement.
Formule du Coefficient de variation
Voici la formule pour calculer le coefficient de variation:
CV = σ / µ
Où: σ est l’écart type et µ est la moyenne.
Veuillez noter que si le rendement attendu du dénominateur de la formule du coefficient de variation est négatif ou nul, le résultat pourrait être trompeur.
Exemple de coefficient de variation pour la sélection des investissements
Fred veut trouver un nouvel investissement pour son portefeuille. Il recherche un investissement sûr offrant des rendements stables. Il considère les options d’investissement suivantes:
Actions: Fred s’est vu proposer des actions de ABC Corp. Il s’agit d’une entreprise mature dotée d’un solide rendement opérationnel et financier. La volatilité du titre est de 10% et le rendement attendu est de 14%.
FNB: Une autre option est le fonds négocié en bourse (FNB) , qui suit la performance de l’indice S & P 500. Le FNB offre un rendement prévu de 13% avec une volatilité de 7%.
Obligations: Les obligations bénéficiant d’une excellente cote de crédit offrent un rendement prévu de 3% avec une volatilité de 2%.
Afin de sélectionner l’opportunité d’investissement la plus appropriée, Fred a décidé de calculer le coefficient de variation de chaque option. En utilisant la formule ci-dessus, il a obtenu les résultats suivants:
Actions: CV= 10/14 = 0,714 = 71,4%
FNB: CV= 7/13 = 0,538 = 53,8%
Obligations: CV= 2/3= 0,667 = 66,7%
Sur la base des calculs ci-dessus, Fred souhaite investir dans les FNB, car ils offrent le coefficient de variation (le plus bas) et le ratio risque / récompense le plus optimal.