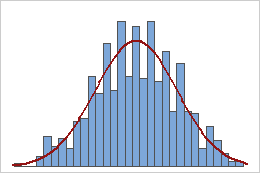
Valeur P
En statistique, la valeur de p est la probabilité d’obtenir les résultats observés d’un test, en supposant que l’hypothèse nulle est correcte. Il s’agit du niveau de signification marginale dans un test d’hypothèse statistique représentant la probabilité d’occurrence d’un événement donné. La valeur de p est utilisée comme alternative aux points de rejet pour fournir le plus petit niveau de signification auquel l’ hypothèse nulle serait rejetée. Une valeur de p plus petite signifie qu’il existe des preuves plus solides en faveur de l’hypothèse alternative.
Comment la valeur P est-elle calculée?
Les valeurs p sont calculées à l’aide de tableaux de valeurs p ou de tableurs / logiciels statistiques. Parce que différents chercheurs utilisent différents niveaux de signification lors de l’examen d’une question, un lecteur peut parfois avoir du mal à comparer les résultats de deux tests différents.
Par exemple, si deux études des rendements de deux actifs particuliers étaient entreprises en utilisant deux niveaux de signification différents, un lecteur ne pourrait pas comparer facilement la probabilité de rendements des deux actifs.
Pour faciliter la comparaison, les chercheurs présentent souvent la valeur de p dans le test d’hypothèse et permettent au lecteur d’interpréter lui-même la signification statistique. C’est ce qu’on appelle une approche de valeur p pour tester les hypothèses.
Approche de la valeur de p aux tests d’hypothèse
L’approche de la valeur de p pour le test d’hypothèse utilise la probabilité calculée pour déterminer s’il existe des preuves pour rejeter l’hypothèse nulle. L’hypothèse nulle, également connue sous le nom de conjecture, est la prétention initiale concernant une population de statistiques.
L’hypothèse alternative indique si le paramètre de population diffère de la valeur du paramètre de population indiquée dans la conjecture. En pratique, la valeur de p, ou valeur critique, est indiquée à l’avance pour déterminer comment la valeur requise pour rejeter l’hypothèse nulle.
Erreur de type I
Une erreur de type I est le faux rejet de l’hypothèse nulle. La probabilité qu’une erreur de type I se produise ou rejette l’hypothèse nulle lorsqu’elle est vraie est équivalente à la valeur critique utilisée. Inversement, la probabilité d’accepter l’hypothèse nulle lorsqu’elle est vraie équivaut à 1 moins la valeur critique.
Exemple réel de valeur P
Supposons qu’un investisseur affirme que la performance de son portefeuille d’investissement est équivalente à celle de l’ indice S&P 500. Pour le déterminer, l’investisseur effectue un test bilatéral. L’hypothèse nulle indique que les rendements du portefeuille sont équivalents aux rendements du S&P 500 sur une période spécifiée, tandis que l’hypothèse alternative stipule que les rendements du portefeuille et les rendements du S&P 500 ne sont pas équivalents. Si l’investisseur effectuait un test unilatéral, l’hypothèse alternative indiquerait que les rendements du portefeuille sont inférieurs ou supérieurs aux rendements du S&P 500.
Une valeur de p couramment utilisée est 0,05. Si l’investisseur conclut que la valeur de p est inférieure à 0,05, il existe des preuves solides contre l’hypothèse nulle. En conséquence, l’investisseur rejetterait l’hypothèse nulle et accepterait l’hypothèse alternative.
À l’inverse, si la valeur de p est supérieure à 0,05, cela indique qu’il existe des preuves faibles contre la conjecture, de sorte que l’investisseur ne rejetterait pas l’hypothèse nulle. Si l’investisseur constate que la valeur de p est de 0,001, il existe des preuves solides contre l’hypothèse nulle, et les rendements du portefeuille et les rendements du S&P 500 peuvent ne pas être équivalents.